
Sadece Ortalama Kitleden Zeki Olanların İdrak Edebileceği Paradoks: Sonsuz Odalı Otel

Sonsuzluk kavramı, zihinsel olarak beynimizi kurcalayan lakin inanmaya akıl erdiremediğimiz bir olgu. Zira insan zihni, bir şeyin sonlarını belirleme eğiliminde olduğundan bir tabirin sonsuz olma fikrini benimsemekte zorlanabiliyor.
Bu sonsuzluk kavramı da 1920’lerden itibaren matematikçileri bu mevzuyu daha anlaşılır bir halde açıklamaya yönlendirdi. Bu uğraşlar arasında en tesirli olanı ise Alman Matematikçi David Hilbert’in “Sonsuz Otel Paradoksu” oldu.
Şimdi bir otel hayal edin. Bu otelin sonsuz tane odası olsun. “Böyle bir şey mümkün değil!” demeden evvel biraz daha düşünmenizi istiyoruz. Üstelik bu sonsuz odaların her biri de dolu. Artık daha karışık geldiğinin farkındayız, daha detaylı bir biçimde ele alınca eminiz ki kafanızda oturacak.
Bir kişi, her odası dolu otelden boş bir oda talep ettiğinde ne olur?
Yeni gelen bir konuğa yapılabilecek şeyi düşündüğümüzde cevap çoğunuzun öngördüğü üzere olacak. Ama bu otelin mantığı biraz daha farklı.
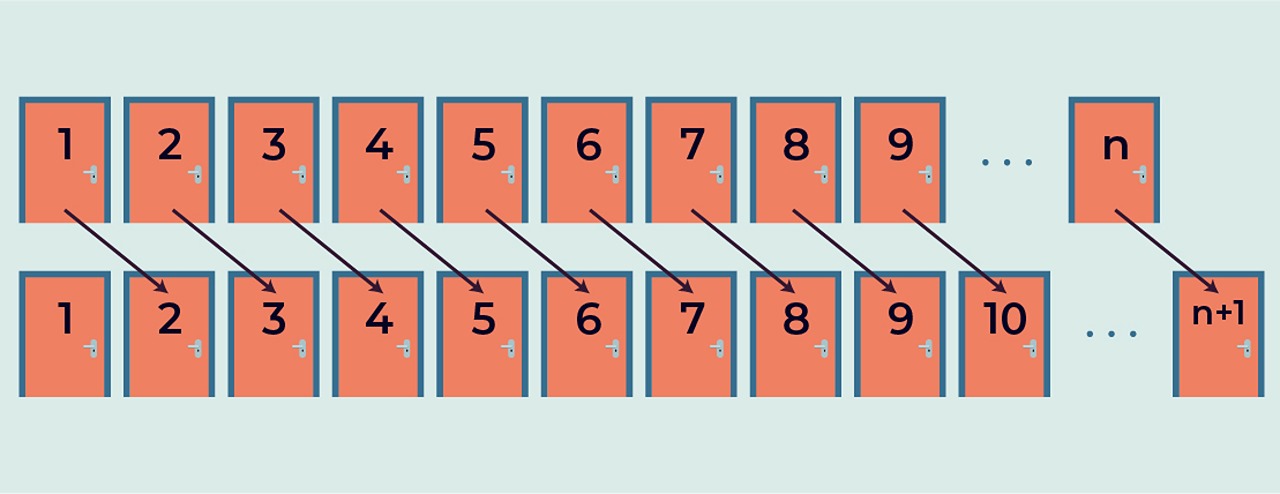
Otel odalarında her konuğun, kendi numarasının bir üstündeki odaya taşınabilme mümkünlüğü var. Yani, 1 numaralı odadaki konuk 2 numaralı odaya taşınırsa 1 numaralı oda boş kalacak ve yeni konuğa yer açılacak.
Peki soruyu biraz daha karmaşıklaştıralım, içinde 40 yolcu bulunan bir otobüs bu otele gelirse nasıl yer ayarlanır?
Pratikte 1 numaralı odadaki konuktan 2 numaralı odaya geçmesi rica edilir, akabinde 2 numaralı odadakinden 3 numaralı odaya ve durum bu formda devam eder.
Otelde sonsuz sayıda oda olduğu için her konuk için yeni bir oda bulmak mümkündür. Bu türlü süren bir döngüde yeni gelen konuk için 1 numaralı oda boşalmış olur.
Aslında mantık yeniden tıpkı.
Ancak bu sefer konuklar, kendi odalarının 40 numara üstüne taşınmalıdır. Yani 1 numaralı odadaki konuk 41 numaralı odaya taşınırsa 2 numaralı odadaki konuk 42 numaralı odaya geçmelidir.
Bu biçimde birinci 40 oda boşalacaktır. Durumu yeterlice karmaşık hâle getirelim mi?
Otobüsü hayal etmiştik, artık de “sonsuz” yolcu sayısı olan bir otobüsle karşılaşılırsa durum nasıl olacak?
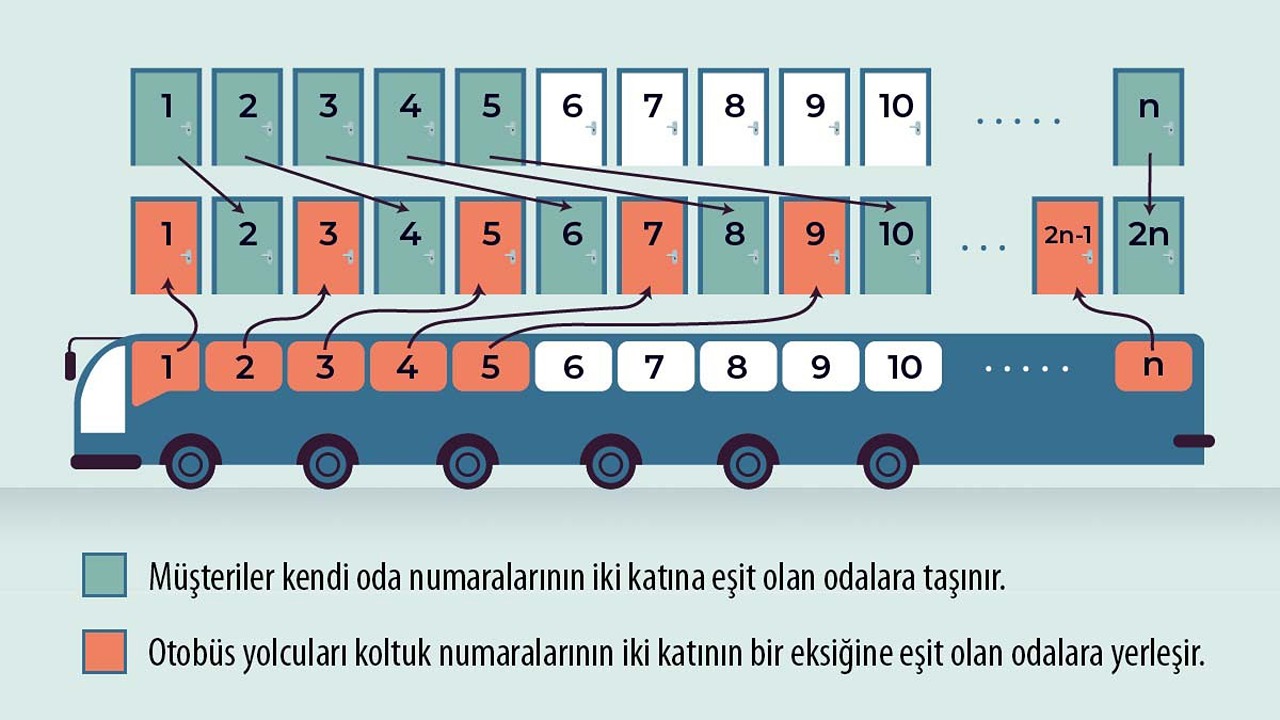
Bu sefer de yeni gelenlerin sayısı bilinmeyen olduğundan ve iç içe geçmiş bir sonsuzluk durumu kelam konusu olduğundan şu çözüm bulunuyor: Her konuğu, oda numarasının iki katı olan bir odaya yerleştirmek.
Yani 1 numaralı konuk 2 numaralı odaya, 4 numaralı konuk 8 numaralı odaya ve bu türlü devam ederek. Bu biçimde, sonsuzluğun içindeki öbür bir sonsuzluğa yer açılmış oluyor.
Böylece oteldeki çift sayılı odalar dolu olurken tek sayılı odalar boş kalır ve gelen konuklar o odalara yerleşebilir. Otelin çıkarı ise bu durumda yeniden sabit kalmış olur.
Mantığı bir defa daha zorlarsak otelin önüne yolcusu sonsuz sayıda olan otobüslerden sonsuz tane gelse ve otelde konaklamak istese yine yer ayarlanabilir mi?
Başlangıçta düşündüğümüz gibi cevap hayır olacak. Çünkü mantıken sonsuz olan bir şeyin içine sonsuz ekleyemeyiz üzere görünüyor.
Ancak oteldekiler, bu duruma “Matematikte sonsuz sayıda asal sayı vardır.” mantığıyla tahlil buluyor. Peki, bu kuralı bu cins bir sorunun içinde nasıl uyguluyorlar?
Aslında yeni konukları otele yerleştirmeden evvel içeride biraz değişiklik yapmaları gerekiyor. Bu değişiklik, asal sayıların en küçüğü 2 olduğundan, otel içindeki bütün müşterileri oda numaralarını 2’nin üssü olacak şekilde yer değiştiriyorlar.
Yani 1 numaralı odadaki müşteri 2¹., 9 numaralı odadaki müşteri 2⁹. odaya taşınıyor. Bu süreçle de otelde boş odalar oluşturuluyor.
Bu otobüslerden birincisindeki yolcuları 3, ikincisindeki 5 biçiminde sırasıyla asal sayı tertibine nazaran yerleştiriyorlar.
Yani ilk otobüsteki birinci yolcu 3¹, ikinci yolcu 3², … numaralı odalara yerleştiriliyor. Tıpkı süreçler diğer asal sayılı otobüslere de uygulanarak sonsuza kadar devam ediyor.
Bu halde tüm müşteriler otele yerleşiyor ve hiçbir oda numarası birbiriyle çakışmıyor. Çünkü asal sayıların sırf 1 ve kendileriyle bölünebilecekleri biliniyor. Hatta otelde boş oda bırakılıyor, 6 yahut 12 numaralı odaların asal sayıların üssü olmadığı için boş kaldığı üzere.
Peki asal sayıların kuvvetlerine eşit oda numaralarının sürekli boş olacağından nasıl eminiz?
Çünkü müspet her tam sayı, asal sayıların çarpımı halinde tek bir şekide yazılabiliyor. Bu durumda da oteldeki bir oda numarası bir asal sayının kuvvetiyse başka asal sayının kuvvetine denk olamaz. Tek asal sayıların hiçbir kuvveti ikiye bölünemez ve bu odalar boş kalır.
Hilbert, bu problem aracılığıyla aslında bize sonsuzluğu anlatmıyor, sonsuzluğu anlamanın ne kadar güç olduğunu ve bu kavramı benimsemek için çeşitli örneklerle hakikat yolu gösteriyor.
Problemlerle ilgili öbür içeriklerimiz:






