

5×5 modülden oluşan bir çikolatanın hakikat oranlarla daima bir kesimini yiyerek sonsuz sayıda çikolataya sahip olabilir misiniz? İnternette dolaşan ve mümkünmüş üzere gösterilen bu paradoksu açıklıyoruz.
Dünya üzerinde en çok hayranı olan yiyeceklerden biri olan çikolatayı çoğumuz seviyoruz. Nasıl yapıldığından içerisine konulan şeylerin oranına nazaran binlerce farklı tatta çikolata bulunuyor. Bir markanın çikolatasıyla öbür markanın çikolatası ortasında bile büyük farklılık var, lakin kaliteli bir çikolatanın ağızda bıraktığı o ağır lezzeti sevmeyen yoktur diye düşünüyoruz.
Çikolatayı bu kadar çok sevdiğimiz için bitmesini istemiyoruz. Pekala aldığınız bir çikolatayı matematiği kullanarak sonsuza kadar çoğaltmak mümkün mü? Elbette bir boyutu ve yükü olan somut bir gıdayı sonsuza kadar yemek mümkün değil ancak matematik, teoride bunu mümkün kulan bir paradoksa sahip.
Çikolatayı yanlışsız bölgelerden bölerek sonsuz sayıda çikolata modülü üretebilir miyiz?
Yukarıdaki görselde de gördüğünüz üzere 5 x 5 modülden oluşan bir çikolatayı düşünelim. Bu çikolatayı muhakkak bir açıyla ortadan ikiye bölelim ve üstte kalan parçayı da yeniden kimi özel modüllere ayıralım. (Çikolatanın nasıl parçalandığını üstteki GIF’ten görebilirsiniz.) Bu formda bir kesim süreci yapıp modüllerin yerlerini değiştirip tekrar koyduğunuzda 1 kesimin dışarıda kaldığını görüyoruz.
Bu açıdan bakıldığında 1 modülün dışarıda kaldığını, üstelik hala 5 x 5 kesimin bütünlüğünü koruduğunu görüyoruz. Bu da bize “Sonsuz çikolataya sahip olabilir miyiz?” sorusunu sorduruyor. Pekala nitekim oluyor mu?
Bir çikolatayı sonsuza kadar parçalayıp yemeyi mümkünmüş üzere gösteren “Banach – Tarski paradoksu” tam olarak nasıl işliyor?

Sonsuz çikolata paradoksu, matematikte yeri olan Banach – Tarski paradoksunun bir örneği aslında. Bu paradoksa nazaran “hiçbir şeyden bir şey var etmek” mümkün. Lakin üstteki görselde her ne kadar gerçekmiş üzere görünse de dünya fiziğinde bir gerçekliği yok. Şayet gerçek dünyada bu usulü uygularsanız çikolatanın boyutunun küçüldüğünü görebilirsiniz. Kısaca üstteki GIF’te bir hile var.
Konuyu daha güzel kavramak için Banach – Tarski paradoksunun kökenine inelim.

1924 yılında Stefan Banach ve Alfred Tarski tarafından ortaya atılan bu matematiksel paradoks, teoride içi dolu bir küreyi sonlu kesimlere ayırıp bu kesimleri eğip bükmek ve germek olmaksızın yalnızca öteleme ve döndürme yolu ile tekrar bir ortaya getirerek orijinal küreyle birebir olan iki küre oluşturmanın matematiksel formülünün mümkün olduğunu gösteriyor.
Bu paradoksta örneğin 1 hacme sahip küreyi ölçülemeyen modüllere bölüyorsunuz. Bu modüller ölçülemez oldukları için tekrar bir ortaya geldiklerinde istediğiniz hacmi alabilmenizi sağlıyor. Bu paradoks elbette gerçek dünyada gerçek sonuç vermiyor. Soyut olan bir dünyada ise matematiksel olarak uygulanabilir oluyor.
Peki görseldeki kayıp nereye gitti?
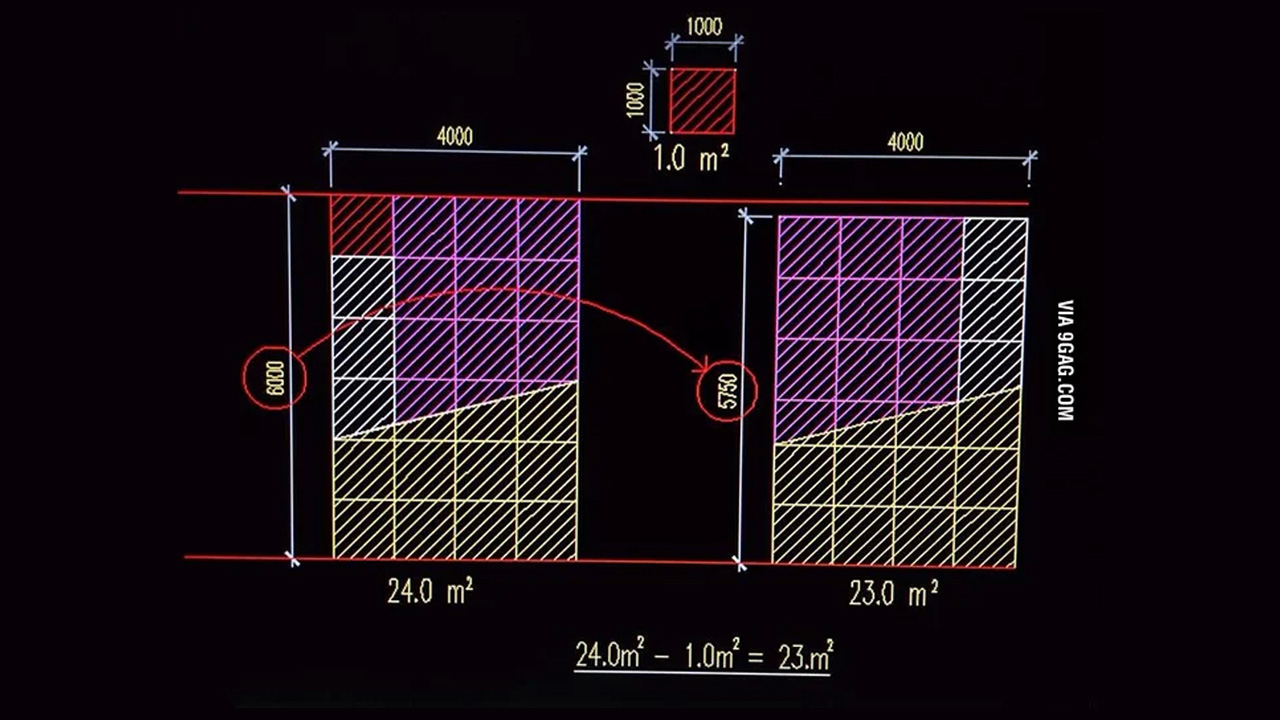
Yukarıda görselde de görebileceğiniz üzere fazlalık olan 1 modül çikolata, çikolatanın kalanından çıkarıldığında yeniden 25 kesim ele edilebiliyor ancak çikolatanın bütününden o 1 kesim çikolatanın alanı daralmış oluyor. Görseldeki bu yanılsama her ne kadar “böyle bir şey mümkün mü?” dedirtse de gerçeklikte maalesef bir çikolatayı sonsuza kadar yemeye devam edemiyoruz.






