

Her birimiz farklı beşerler olsak da ortak paydada buluştuğumuz bir nokta var ki o da hislerimiz. O denli ya da bu türlü hayatımızın birçoklarını “gerçek aşkı bulmak” için harcıyoruz ve bu mutlak memnunluğu elde edebilmenin yollarını arıyoruz. Pekala matematikçiler ruh eşinizi bulmanız için size yardımcı olmayı düşünüyor desek?
Matematik yaygın bilinenin tersine sadece soyut ve çözmesi güç sorunlardan oluşmuyor. Bu bilim kısmı, aslında hayatımızın birçok yerinde bizimle birlikte ve hesaplanmasının mümkün olmadığını düşündüğümüz bahislerde bile öngörüleriyle bizi aydınlatabiliyor.
Bu bağlamda aşkın matematiğinin ne biçimde işlediğine ve matematiğin, bu manada bize nasıl yardımcı olduğuna bakalım.
Uzun müddettir bekar bir matematikçi olan Peter Backus, “Neden Bir Kız Arkadaşım Yok” başlıklı bir makale kaleme alır.

Backus’un bu çalışması, ismini yaratıcısı Frank Drake’ten alır ve Drake denkleminden faydalanarak oluşturulur. Gökbilimci Frank Drake, 1961’de cihan içerisinde yalnız olup olmadığımızı anlayabilmemiz için bir çeşit niyet deneyi gerçekleştirmişti. Drake, kozmostaki teknolojik manada gelişmiş uygarlıkların sayısının, yedi değişkenin bir eseri olacağını öne sürmüş ve denklemini bu bağlamda oluşturmuştu.
Backus da bu fikirden yola çıktı ve çalışmasının sonunda galaksideki uyarlık sayısının, onun potansiyel kız arkadaşı sayısından daha fazla olduğunu hesapladı zira İngiltere’deki 30 milyon bayan içinde sadece 26 tanesi ile sevgili olabileceğini tespit etmişti.
Bu durumda mümkünlük “milyonda bir” kadardı.
Tabii ki tam manasıyla kaç tane uzaylı hayat formu olduğunu hesaplamanın mümkün olmadığı gibi kesin olarak kaç potansiyel partnerimizin olabileceğini hesaplamak da mümkün değil fakat yeniden de bu sayılar net bir formda tespit edilemese de iddiada bulunabilme gücü, bir bilim insanı için epey pahalı.
Backus, bu çalışmadan evvel, aradığı beşere dair kendince bir kadro kriterler belirledi ve akabinde bu ölçütleri tıpkı Drake üzere 7’ye indirdi. Böylece probleme bir bütün olarak bakmaktan fazla modüller üzerinden giderek karşılık verebilecekti.
Gelelim Backus’un kendi partnerini bulabilmek için belirlediği 7 kritere:
- Yakınımda yaşayan kaç bayan var? (Londra’da -> 4 milyon kadın)
- Kaç kişi doğru yaş aralığında olabilir? (%20 -> 800.000 kadın)
- Kaçının bekar olma ihtimali var? (%50 -> 400.000 kadın)
- Kaçının üniversite diplomasına sahip olma mümkünlüğü var? (% 26 -> 104.000 kadın)
- Kaçı bana çekici gelebilir? (%5 -> 5.200 kadın)
- Kaçı beni çekici bulabilir? (%5 -> 260 kadın)
- Kaç tanesiyle yeterli anlaşabilirim? (%10 -> 26 kadın)
Bu ortada belirtmek gerekir ki Backus İngiltere’de yaşıyordu ve ölçütlerinin kimilerini yaşadığı coğrafyaya nazaran belirlemişti. Elbette biz de bu kriterleri Türkiye odaklı düşünebiliriz.
Backus elbette bu kadar seçici olmasaydı ve ölçütlerinden kimilerinin hudutlarını biraz daha genişletseydi bu sayı artabilirdi.
Örneğin aradığı bayanı sadece Londra’da değil de dünyanın öbür ülkelerinde de bulabilme üzere bir isteği olsaydı, bahtı anında birkaç katına çıkabilirdi. Tekrar gelecekteki aşkının üniversite mezunu olmasına takılmayıp, bu hududu biraz daha genişletseydi de elde ettiği oranda bir epey yükseliş olacaktı.
Aslında uzayıp gitmesi daha da mümkün olan bu türlü bir liste oluşturmak, bir nebze imkansıza meydan okumaktan farksız. Bunun yerine gerçekten olmazsa olmaz birkaç kriter belirleyip, sırf onlarla sonlu kalmak ve bunun yanında etrafımızdakilere istedikleri bahtı bir kere olsun vermek aradığımız gerçek insanı bulma noktasında yardımcı olabilir.
Aşkın matematiğini ele aldığımız bir başka çalışmada ise matematikçiler, bir bağlantının sürüp sürmemesini matematiksel manada hesaplamaya çalıştı.
Elbette her alakada kesinlikle çatışmalar vardır lakin bu sorunlarla gerçek bir halde başa çıkmak için, birtakım araçlara gereksinim duyarız. Bu noktada ilgilerde ortaya çıkan matematiksel kalıplar birtakım öngörüler verebilir.
Örneğin psikolog John Gottman ve takımı bir çalışmasında, birkaç on yıl boyunca neredeyse yüzlerce çiftin ileşimini gözlemledi. Bu şahısların yüz sözleri, kan basınçları ve kalp atış hızları üzere tespit edebildikleri tüm kıymetleri ölçüldü.
Ardından Gottman ve takımı bir puanlama sistemi ile bu çiftlerin yaklaşık %90’a varan bir doğruluk hissesiyle ayrılıp ayrılmayacaklarını evvelden varsayım edebildiklerini ortaya koydu. Tüm bu çalışmalara gerisinden matematikçi James Murray dahil oldu ve tüm bu bilgileri tahlil ederek bir matematiksel model elde etti.
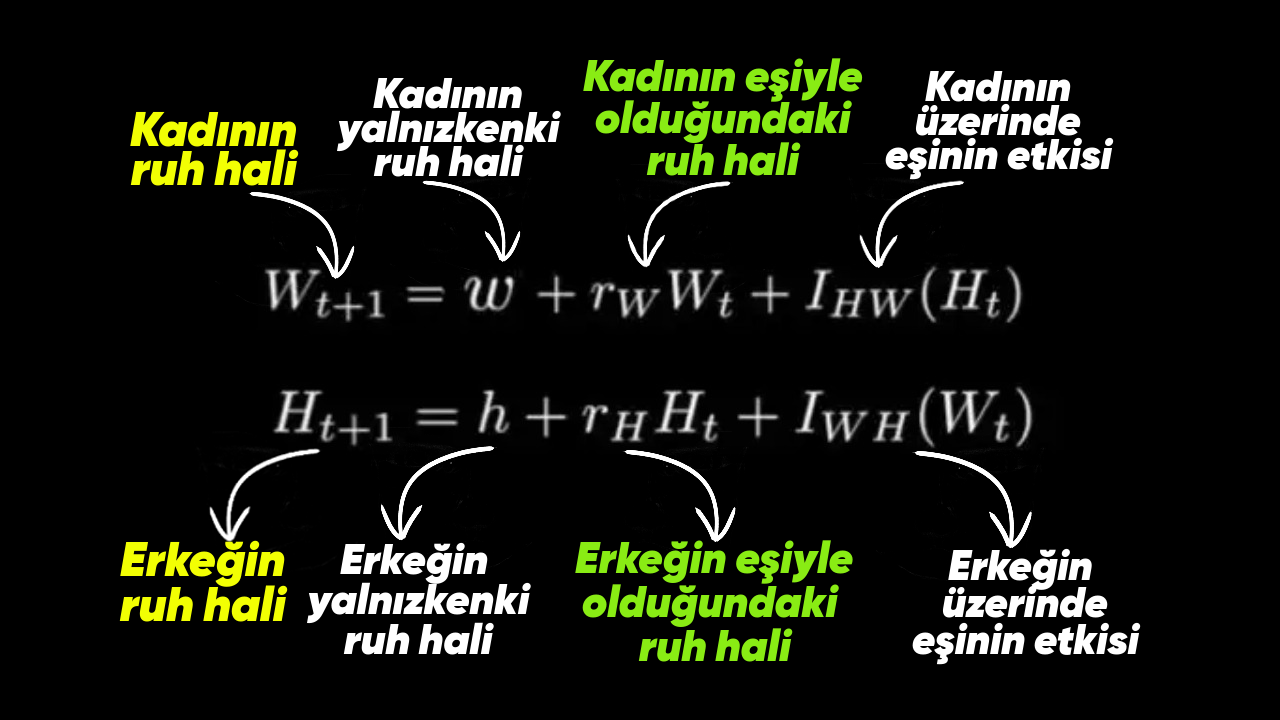
Matematikçi, bir bağın akıbetini kendince bu iki denklemle özetleme yoluna gitti.

Bu denklemler birinci etapta anlamsız üzere görünse de aslında çiftlerin birbirleriyle olan konuşmalarının bir sonraki basamakta ne kadar olumlu yahut olumsuz olacağını varsayım etme manasında bir kurallar bütününü söz etmekte. Üst satır bayanı için oluşturulurken, alt satır da erkekleri temsil eder.
İlk denklemin sol taraftan başlayan kısmı, bayanın bir sonraki söyleyeceği sözlerin ne kadar olumlu yahut olumsuz olacağıdır. Bayanın yansısı genel manada ruh haline (w), eşiyle birlikteyken ilişkin hissettiği ruh haline (rwWt) ve son olarak en bariz ölçüt olarak eşinin aksiyonlarının onun üzerindeki tesirine (IHM) bağlıdır.
Denklemin sonundaki Ht de bu tesirin bir bakıma eşinin az evvel ne yaptığına bağlı olduğunu tabir etmenin matematiksel kısaltmasıdır. Tıpkı mantık, alt satırda erkek için tanımlanır.
Aslında alakanın devam etme müddeti iki partnerin birbirini nasıl etkilediğine bağlıdır ve bu bağlamda Gottman ve Murray’in denklemlerindeki en bariz öge, tesir terimidir.
Bir erkeğin (Ht), eşi (IHM) üzerindeki tesiri kılavuz olarak alındığında ve bu denklemin yüksek kıymetlerle sonuçlandığı her durumda, ikili ortasında olumlu bir etkileşim bulunduğu görülür. Ancak bu paha sıfırın altına düşerse, eşin konuşmadaki bir sonraki kelamının olumsuz olma ihtimali daha yüksektir.
Konuyu bayan açısından da değerlendirelim ve erkeğin tartışma sırasında olumlu davranışlar sergilediği varsayalım. Örneğin eşinin kelamını onaylaması ya da ortamın gerginliğini dağıtmak için espri yapması üzere. Bu aksiyon, bayan üzerinde küçük de olsa olumlu bir tesir yaratacak ve karşısındakine daha olumlu karşılık verme ihtimalini arttıracaktır.
Eğer erkek tam da tartışma esnasında, eşine onu sevdiğini söylemek üzere bir yaklaşımda bulunursa da T+ noktasına ulaşılır. Bu dakikadan sonra, çiftin ortasındaki tartışmanın tatlıya bağlandığını görmek muhtemel olacaktır.
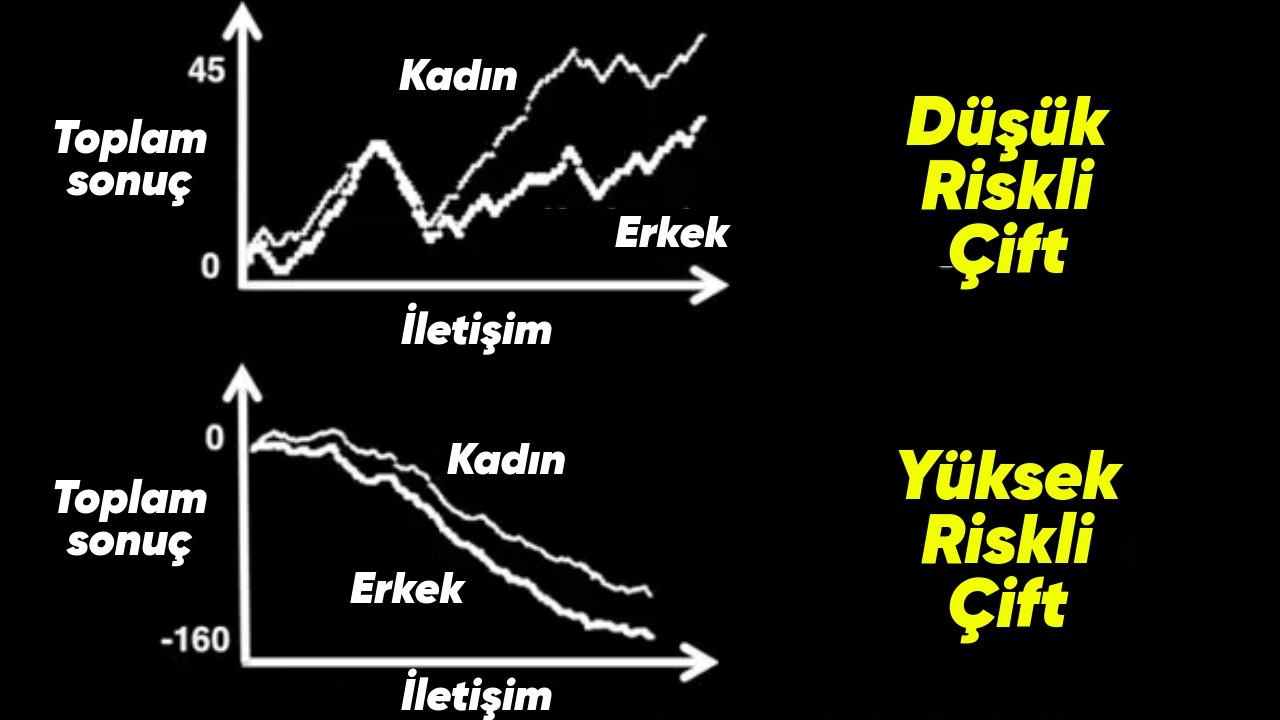
Aksine erkek bağlantı esnasında eşinin kelamını kesmek gibi olumsuz bir hal sergilediğinde ise bu durumun, eşi üzerinde sabit ve olumsuz bir tesiri olacaktır. Bu gidişatta da çift, nihayetinde “olumsuzluk eşiği” olarak isimlendirilen noktaya ulaşması epeyce yüksek bir ihtimaldir.
En başarısız ilişkilerdeki olumsuzluk eşiklerinin önemli manada yüksek olduğunu söylemek mümkün olur. Bu bağlarda çiftler birbirine tahammülsüzdür ve ortalarındaki en küçük sorunu bile tahlile kavuşturamazlar.

Aşk ilgilerini matematik bağlamında ele almak, bize kimi vakit neden yalnız olduğumuzun yanıtını verebilirken; bazen de ilişkimizdeki gidişatı sağlam temellerle devam ettirme noktasında hayli yardımcı olabilir. Şayet siz de bu sorunun yanıtını arıyorsanız, matematiğe bir danışın deriz.






